The Fundamentals of Linear Programming: Theory and Practice

Linear programming is a mathematical technique that allows for the optimization of a linear objective function subject to linear constraints. This technique is widely used in various fields such as business, economics, engineering, and even social sciences. In this article, we will discuss the fundamentals of linear programming theory and practice.

Linear Programming Problem Formulation

The first step in solving a linear programming problem is to formulate the problem. This involves identifying the decision variables, the objective function, and the constraints. The decision variables are the unknown quantities that we want to determine. The objective function is the function that we want to optimize, and the constraints are the limitations on the decision variables.

Linear Programming Solution Methodology

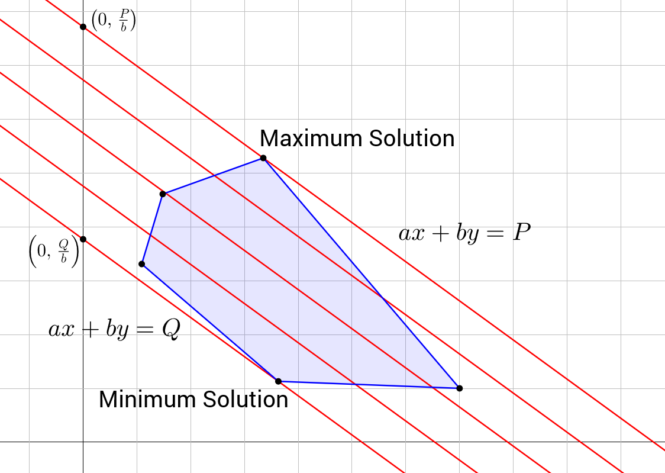
Linear programming (LP) is a powerful mathematical technique that allows for the optimization of a linear objective function subject to linear constraints.

Formulating the Problem

The first step in solving a linear programming problem is to formulate the problem. This involves identifying the decision variables, the objective function, and the constraints. The decision variables are the unknown quantities that we want to determine. The objective function is the function that we want to optimize, and the constraints are the limitations on the decision variables.

Sensitivity Analysis

Sensitivity analysis is an important technique in linear programming (LP) that allows for the examination of how changes in the parameters of the LP problem affect the optimal solution.

Defining Sensitivity Analysis

Sensitivity analysis involves examining how changes in the parameters of the LP problem, such as the coefficients of the objective function or the right-hand side of the constraints, affect the optimal solution. The goal of sensitivity analysis is to determine how sensitive the optimal solution is to changes in the problem parameters.

Applications of Sensitivity Analysis

Sensitivity analysis has numerous applications, including risk assessment, decision-making, and forecasting. In risk assessment, sensitivity analysis can be used to determine the impact of uncertainty on the optimal solution. In decision-making, sensitivity analysis can be used to examine the effect of changes in the problem parameters on the optimal decision. In forecasting, sensitivity analysis can be used to determine the range of values for the problem parameters that will result in an optimal solution.

Interpreting Sensitivity Analysis Results

The results of sensitivity analysis are typically presented in the form of sensitivity reports or graphs. These reports or graphs show how changes in the problem parameters affect the optimal solution. Sensitivity analysis can help decision-makers understand the trade-offs between different decision options and the impact of changes in the problem parameters on the optimal decision.

Duality in Linear Programming

Duality is an important concept in linear programming (LP) that relates the primal problem to its corresponding dual problem.

The Primal Problem and its Dual

The primal problem in LP is the problem of maximizing or minimizing a linear objective function subject to linear constraints. The dual problem is obtained by formulating a new problem that has the same constraints as the primal problem but a different objective function. The dual problem is formulated in such a way that it provides information about the primal problem, such as the range of possible values for the objective function.

Relationship Between the Primal and Dual Problems

The relationship between the primal and dual problems is based on the principle of complementary slackness. This principle states that the optimal solutions to the primal and dual problems are related in such a way that the product of the slack variables is zero. In other words, if a constraint in the primal problem is not binding, then the corresponding variable in the dual problem will be zero, and vice versa.

Applications of Duality in LP

Duality in LP has numerous applications, including sensitivity analysis, resource allocation, and model building. The dual problem can be used to provide additional information about the primal problem, such as the shadow prices of the constraints, which indicate how much the value of the objective function will change with a unit increase in the right-hand side of the constraint.

Applications of Linear Programming

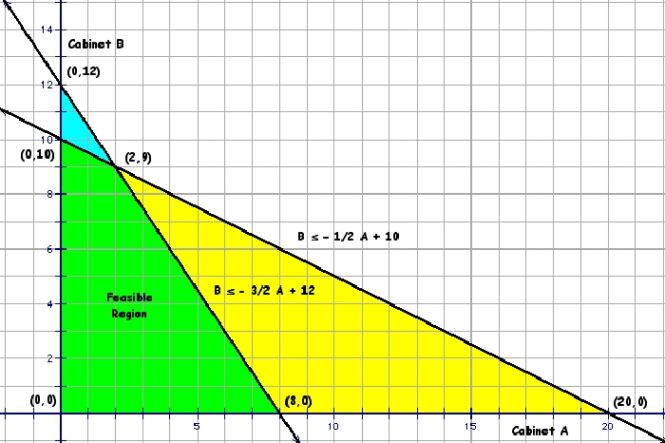
Linear programming (LP) is a powerful mathematical technique that has numerous applications in various fields. LP allows for the optimization of a linear objective function subject to linear constraints, making it a useful tool for decision-making and optimization in various industries.

Production Planning and Inventory Management

LP is widely used in manufacturing industries for production planning and inventory management. LP models can be used to optimize production schedules, minimize costs, and maximize profits while meeting production demands and inventory requirements. LP can help manufacturers minimize the cost of production while ensuring that they have the necessary inventory to meet customer demands.

Transportation and Logistics

In the transportation and logistics industry, LP is used for route optimization and scheduling. LP models can be used to determine the optimal routes for transporting goods and services, minimizing transportation costs, and maximizing efficiency. LP can also be used to schedule the delivery of goods and services, ensuring that they are delivered on time and within budget.

Finance and Investment

LP is also widely used in finance and investment for portfolio optimization and risk management. LP models can be used to determine the optimal portfolio of investments that maximizes returns while minimizing risk. LP can also be used to model the impact of various economic and financial factors on investment portfolios and risk management strategies.

Energy and Utilities

LP is used in the energy and utilities industry for energy production and distribution planning. LP models can be used to determine the optimal production levels for different energy sources, such as oil, gas, and renewable energy sources. LP can also be used to optimize the distribution of energy resources, ensuring that they are distributed efficiently and effectively.

Conclusion

Linear programming is a powerful mathematical technique that allows for the optimization of a linear objective function subject to linear constraints. It has numerous applications in various fields such as economics, finance, transportation, and manufacturing. By understanding the fundamentals of linear programming theory and practice, we can make better decisions and optimize our processes for greater efficiency and effectiveness.